Circunferencia

Caracteristicas, área y perímetro

¿Qué es una circunferencia?

La circunferencia es una línea curva, cerrada y plana,

cuyos puntos están todos a la misma distancia de otro punto,

llamado centro.
Dimensión de la circunferencia:

Al ser una línea, la circunferencia tiene una sola dimensión, la longitud.

La longitud de una circunferencia:

Una circunferencia está formada por:

- Centro de la circunferencia: punto del que equidistan todos los puntos de la circunferencia.

- Radio de la circunferencia: segmento que une el centro de la circunferencia con cualquier punto de la misma.

- Cuerda de la circunferencia: segmento que une dos puntos de la circunferencia, el radio es perpendicular a la cuerda en su punto medio.

- Diámetro de la circunferencia: es una cuerda que pasa por el centro. Es la cuerda que mayor tamaño tiene.

- Arco de la circunferencia: es la porción de circunferencia limitada por dos puntos de la misma, también se puede decir que es cada una de las partes en que una cuerda divide a la circunferencia.

Posiciones relativas de una recta y una circunferencia

Una recta puede estar respecto a una circunferencia:

- Recta exterior: cuando no tiene ningún punto común con la circunferencia.
- Recta tangente: a la circunferencia cuando tiene un punto común.
- Recta secante: a la circunferencia cuando tiene dos puntos comunes .

Posiciones relativas de dos circunferencias:

- Circunferencias exteriores: son las que no tienen ningún punto en común y cada una esta en una región exterior a la otra.

- Circunferencias interiores: no tienen ningún punto en común y una está en la región interior de la otra.

- Circunferencias tangentes exteriores: tienen un punto en común y los demás puntos de cada una de ellas están en la región exterior de la otra.

- Circunferencias tangentes interiores: tienen un punto en común y los demás puntos de una de ellas están en la región interior de la otra.

- Circunferencias secantes: tienen dos puntos en común.

- Circunferencias concéntricas: no tienen ningún punto en común, una esta en el interior

de la otra y tienen el mismo centro pero distinto radio.

Ángulos de la circunferencia:

- Ángulo central: es el ángulo que tiene su vértice en el centro y sus lados lo forman dos radios. Si dos ángulos centrales son iguales también lo son los arcos correspondientes.
La medida de un arco central es la misma que la de su ángulo central correspondiente.

- Ángulo inscrito: es aquel que tiene su vértice en la circunferencia y sus lados son secantes a ella. La medida de un ángulo inscrito es igual a la mitad del arco que abarca.

- Ángulo semi-inscrito: es aquel que tiene su vértice en un punto de la circunferencia y un lado es tangente y el otro secante a ella. La medida de un ángulo semi-inscrito es la mitad del arco que abarca.

- Ángulo interior: es aquel que tiene su vértice en un punto interior del circulo. Sus lados con cuerdas de la circunferencia. Un ángulo interior mide la mitad de la suma de las medias de su arcos que abarcan sus lados y las prolongaciones de los mismos.

- Ángulo exterior: es aquel que tiene su vértice en un punto fuera de la circunferencia y del circulo y su lados son secantes o tangentes de la circunferencia. La medida de un ángulo exterior es la mitad de la diferencia de los arcos que abarca el ángulo.

Área y perímetro

El área es la medida de la región interior de cada cara. Entonces, el área total de un cuerpo redondo corresponderá a la suma de las áreas de todas sus caras. Como los cuerpos redondos tienen caras curvas, vamos a recordar el cálculo del perímetro de una circunferencia y del área de un círculo.

Perímetro de una circunferencia

Corresponde a la longitud que tiene una circunferencia. En esta medida interviene un decimal infinito conocido como (pi) y que equivale a 3,14.... El perímetro de una circunferencia corresponde al producto del doble del radio por , por lo que su fórmula es:

y r = radio de la circunferencia

Veamos un ejemplo. Si una circunferencia tiene 4 cm. de radio, su perímetro es:

Área de un círculo

La circunferencia es la línea curva cerrada en la que cada punto equidista de otro llamado centro. En cambio círculo es la región interior de la circunferencia. Es al círculo al que se le calcula el área. También debemos utilizar la magnitud, siendo su fórmula:

r = radio de la circunferencia.
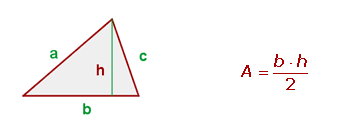
Si queremos saber el área del círculo anterior aplicamos la fórmula:

Repasando lo aprendido.

Actividad

Organiza grupos de cuatro personas, para poder participar debes tener un cuaderno cuadriculado, lápices y regla.

1. Tiene sus cuatro lados iguales, esto se refiere a:

a) El cuadrado
b) Rectángulos
c) El cuadrado y el rombo.

2. Sus tres lados son de distintas medidas, lo anterior señala la descripción de:

a) Triangulo escaleno
b) Triangulo equilátero

c) Triangulo isósceles.

3. Figura de cuatro lados cuyos ángulos miden 90°, es

a) Rectángulo
b) Romboide
c) Cuadrado

4. ¿Cuál de estos no corresponde a un paralelogramo?

a) Rombo
b) Rectángulo
c) Trapezoide

5. Ángulo extendido mide

a) 180°
b) 90°
c) Es mayor a 0° y menor que 90°

6. El ángulo recto mide

a) Mas de 0° y menos que 90°
b) Más de 90° y menos de 180°
c) 90°.

Escribe el nombre según corresponda

Area y perímetro, Triangulo y cuadrilátero

Triangulo

Los triángulos se clasifican según la medida de sus lados en:

Triángulo equilátero

El que tiene sus 3 lados iguales.

Triángulo isósceles

El que tiene 2 de sus lados de igual medida.

Triángulo Escaleno

El que tiene sus 3 lados de distinta medida.

Perímetro de un triángulo

El perímetro de un triángulo es igual a la suma de sus tres lados.

Área de un triángulo

El área de un triángulo es igual a base por altura partido por 2.
La altura es la recta perpendicular trazada desde un vértice al lado opuesto.

Cuadrilátero

Polígono de cuatro lados.

Tipos de cuadriláteros

Paralelogramos

Otra clasificación de los cuadriláteros es la siguiente:

Trapecios: son aquellos que tienen 1 par de lados paralelos.

Trapecio isósceles: 2 lados de igual medida, 2 ángulos basales iguales.

Trapecio trisolátero: 3 lados de igual medida, 2 pares de ángulos basales iguales.

Trapecio rectángulo: ángulos basales rectos (90º).

Trapecio escaleno: lados y ángulos de distinta medida.

Trapezoides: No tienen lados paralelos.

Trapezoide simétrico: 2 lados de igual medida.

Trapezoide asimétrico: todos los lados de distinta medida.

Área y perímetro

El perímetro de un cuadrilátero es la longitud de la línea cerrada que lo bordea, es decir, la suma de las longitudes de sus cuatro lados.

- El área de un rectángulo de lados b y a mide A = b*a (Área = base * altura)

- El área de un paralelogramo cualquiera es A = base * altura

¡A conocer los polígonos!

¿Qué es un polígono?

Los polígonos son figuras cerradas, formadas por varios segmentos de líneas, a las que llamamos lados.

Existen dos tipos de polígonos…

Polígonos regulares

Polígonos irregulares

De acuerdo con sus ángulos interiores, los polígonos pueden ser convexos y cóncavos.

Polígonos Cóncavos y Convexos

Un polígono es convexo si todos sus ángulos interiores son menores de 180º.

Un polígono cóncavo si al menos uno de sus ángulos interiores mide más de 180º.

¿Tienen nombres distintos los polígonos?

Dependiendo del número de lados que tenga la figura, recibirá un nombre distinto.

Thales de Mileto

Se le llamó Tales de Mileto (o Thales) porque vivió en la ciudad de Mileto, entre 624 a.C. - 546 a.C. Fue uno de los "siete sabios" de la antigüedad. Filósofo de la Escuela Jónica, autor de una cosmología de la que sólo nos han llegado algunos fragmentos.

Se destacó principalmente por sus trabajos en filosofía y matemáticas. En esta última ciencia, se le atribuyen las primeras "demostraciones" de teoremas geométricos mediante el razonamiento lógico y, por esto, se la considera el Padre de la Geometría.

Según Tales, el principio original de todas las cosas es el agua, de la que todo procede y a la que todo vuelve otra vez. Se atribuye a Tales el uso de sus conocimientos de geometría para medir las dimensiones de las pirámides de Egipto y calcular la distancia desde la costa hasta barcos en alta mar.

Teoremas de Tales

Una aplicación del Teorema de Tales

A Tales se le atribuyen los cinco teoremas siguientes:

- Los ángulos de la base de un triángulo isósceles son iguales.
- Un círculo es bisecado por algún diámetro.
- Los ángulos entre dos líneas rectas que se cortan son iguales.
- Dos triángulos son congruentes si ellos tienen dos ángulos y un lado igual.
- Todo ángulo inscrito en una semicircunferencia es recto.

A continuación veremos los dos más importantes.

Primer teorema de Tales

Sean dos rectas (d) y (d') orientadas y concurrentes en un punto O. Sean A y A' dos puntos de (d), y B y B' dos puntos de (d'). Entonces:

Segundo teorema de Tales

OA = OB = OC = r, radio del círculo. Por lo tanto OAC y OBC son isósceles. La suma de los ángulos del triángulo ABC vale 2α + 2β = π (radianes). Dividiendo por dos, se obtiene: = α + β = π/2.

Otros teoremas de Tales

Transformaciones Isométricas

Estas son aquellas transformaciones de las figuras en el plano,

no varían sus dimensiones, ni menos su área.

Las figuras son iguales, ya sea la inicial como la final, es decir son congruentes.
Existen tres tipos de isometrías.

En una Simetría Axial

- Cada punto y su imagen equidistan del eje de simetría.
- El trazo que une un punto con su simétrico es perpendicular al eje de simetría.

En una Simetría Central

El centro de rotación es el punto medio del trazo que une un punto con su simétrico.
Además esta es equivalente a una rotación con un ángulo de 180º.

Traslaciones

En una traslación se distinguen tres elementos

Rotación

Se identifican tres elementos:

Apliquemos lo aprendido:

¿Qué rotación es la que observas?

1)

2)

3)

Ángulos y sus clasificaciones

ÁNGULOS

Es la figura formada por 2 semirrectas que parten de un mismo punto.

Las semirrectas se llaman lados y el punto común vértice.

Un ángulo se denota de la siguiente forma:

Clasificación de los Ángulos

Los ángulos pueden clasificarse según su medida en 5 tipos:

Los esquemas que representan dichos ángulos son los siguientes:

OBSERVEMOS BIEN

Las líneas que conforman cada dígito determina, justamente, el número de ángulos que se quiere contar; es decir, el 1 tiene un ángulo, el 2 tiene dos ángulos, el 3 tiene tres, etc.

JUGUEMOS

1) ¿Cuántos ángulos encuentras en cada dibujo?

2) ¿Qué ángulo encuentras?

3) Indica donde esta cada ángulo

¿Cuántos ángulos encuentras en el dibujo?

¡Observa bien!